Categorical Statistics

Introduction

In 1973, a large cotton textile company in North Carolina participated in a study to investigate the prevalence of byssinosis, a form of pneumoconiosis to which workers exposed to cotton dust are subject. Data was collected on 5,419 workers, including:

• Type of work place [1 (most dusty), 2 (less dusty), 3 (least dusty)]
• Employment, years [< 10, 10-19, 20-]
• Smoking [Smoker, or not in last 5 years]
• Sex [Male, Female]
• Race [White, Other]
• Byssinosis [Yes, No]

In this report, I will aim to evaluate the effect of the level of dust in the work place, length of employment, smoking status, sex, and / or race has on the odds that a person will get byssinosis. In order to analyze this data, I will make use of categorical data analysis methods, due to the categorical nature of which this data was collected. Before any analysis was made, it would first be important to set the variable of type of work place as a factor with levels of 1, 2, and 3. After understanding the nature of what this data looks like I will move to fit a model to the given data, as well as, make inference on which of the predicted variables recorded offer a significant effect on the presence of byssinosis in a given subject. Our goal in using model fitting in this way would be to make further predictions on a person’s risk for contracting the disease if more data were to be collected.

Explotatory Data Analysis

We’ll begin our analysis by looking at a descriptive summary of the data collected. To accomplish this, I can look at a plot of multiple boxplots measuring byssinosis by one predictor split up by its levels:

library(ggplot2)
library(plyr)
library(gridExtra)
b.data = read.csv("Byssinosis.csv")
b.data$Workspace = as.factor(b.data$Workspace)

plot1 <- ggplot(data = b.data, mapping = aes(x = Workspace, y = Byssinosis)) +
  labs(title="Byssinosis by Dustyness of Workspace",x="type of workspace", y = "# subjects with Byssinosis") +
  theme_classic() +
  geom_boxplot()
plot2 <- ggplot(data = b.data, mapping = aes(x = Employment, y = Byssinosis), main = "Bysinosis status by Employment length") +
  labs(title="Byssinosis by Length of Employment",x="length of employment (years)", y = "# subjects with Byssinosis") +
  theme_classic() +
  geom_boxplot()
plot3 <- ggplot(data = b.data, mapping = aes(x = Smoking, y = Byssinosis)) +
  labs(title="Byssinosis by Smoking Status",x="smoking status", y = "# subjects with Byssinosis") +
  theme_classic() +
  geom_boxplot()
plot4 <- ggplot(data = b.data, mapping = aes(x = Sex, y = Byssinosis)) +
  labs(title="Byssinosis by Sex",x="sex", y = "# subjects with Byssinosis") +
  theme_classic() +
  geom_boxplot()
plot5 <- ggplot(data = b.data, mapping = aes(x = Race, y = Byssinosis)) +
  labs(title="Byssinosis by Race",x="race", y = "# subjects with Byssinosis") +
  theme_classic() +
  geom_boxplot()
grid.arrange(plot1,plot2,plot3,plot4,plot5, ncol=3)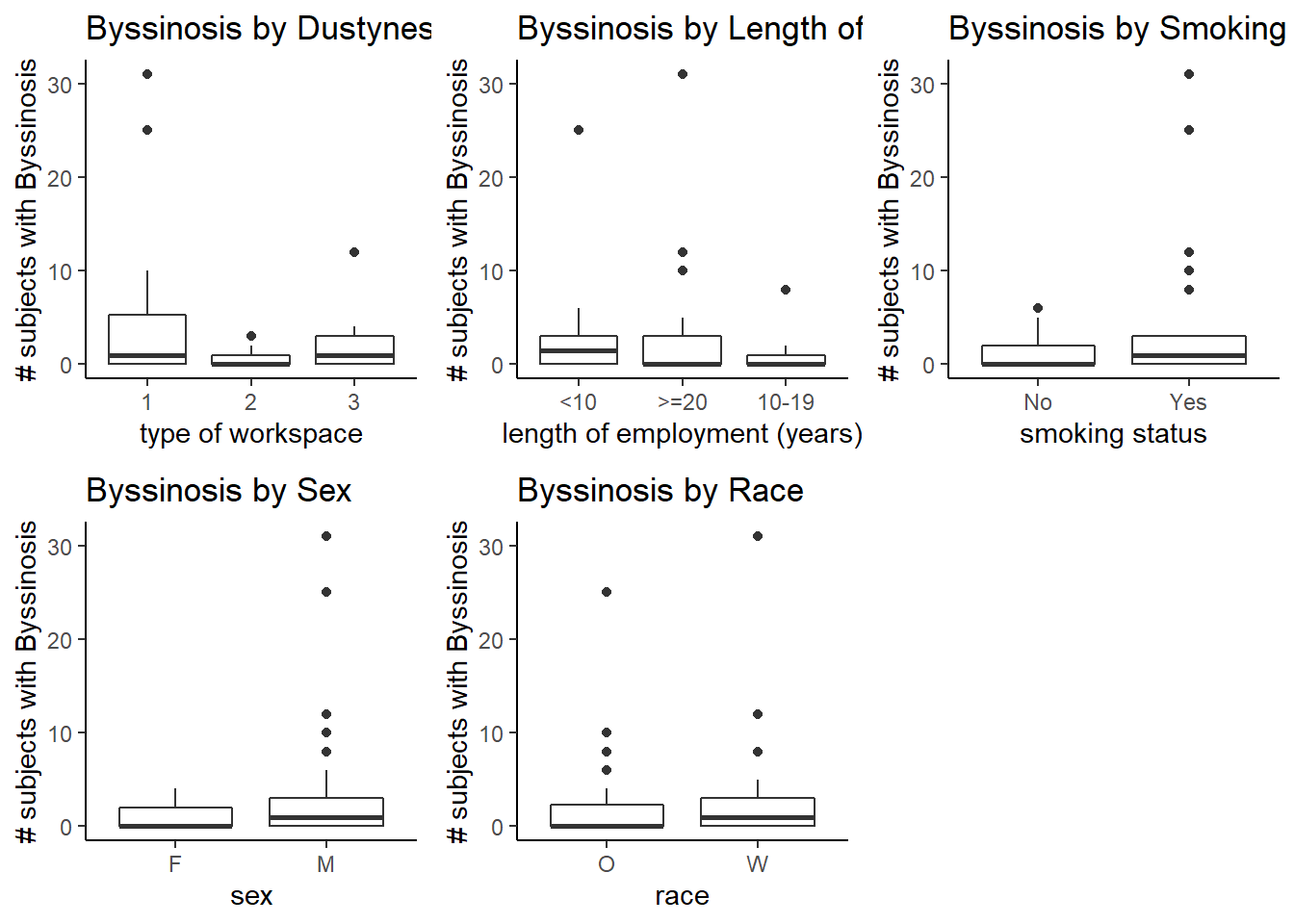

Figure 1 gives us a general idea of the spread of the data by variable and factor level. From this plot, I am able to see which variables have different distributions between its factor levels. The difference in distribution across factor levels may give us a hint as to which variables are going to be important to us later on during model selection. For example, as displayed in Figure 1, the variable race had factor levels white and other, it appears that both levels have roughly the same distribution of number of subjects that were diagnosed with byssinosis. Just from this I could guess that race is not going to have a significant effect on byssinosis. Similar assumptions could be made, but more inferential statistics will have to be done to make any significant conclusions.

Moving on in our exploration of this data, a model can be fit that will help predict a subject’s byssinosis status given these predictors, and whether or not the predictor adds a significant effect to the odds of having byssinosis. To do so, I choose to start with a generalized additive linear model for the log odds of having byssinosis. Wald test p-values were calculated for each predictor, and all but race and sex showed significant at level 0.01 or lower, but further model selection techniques can be conducted in order to determine which predictors to include in our final model

fullModel = glm(cbind(Byssinosis,Non.Byssinosis) ~., data = b.data,family = binomial())
nullModel = glm(cbind(Byssinosis,Non.Byssinosis) ~ 1, data = b.data,family = binomial())
summary(fullModel)
## 
## Call:
## glm(formula = cbind(Byssinosis, Non.Byssinosis) ~ ., family = binomial(), 
##     data = b.data)
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -1.5240  -0.8105  -0.1952   0.2071   1.5643  
## 
## Coefficients:
##                 Estimate Std. Error z value Pr(>|z|)    
## (Intercept)      -2.3463     0.2639  -8.891  < 2e-16 ***
## Employment>=20    0.7531     0.2161   3.484 0.000493 ***
## Employment10-19   0.5641     0.2617   2.156 0.031091 *  
## SmokingYes        0.6413     0.1944   3.299 0.000971 ***
## SexM             -0.1239     0.2288  -0.542 0.587983    
## RaceW            -0.1163     0.2072  -0.562 0.574426    
## Workspace2       -2.5799     0.2921  -8.834  < 2e-16 ***
## Workspace3       -2.7306     0.2153 -12.681  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 322.527  on 64  degrees of freedom
## Residual deviance:  43.271  on 57  degrees of freedom
## AIC: 165.95
## 
## Number of Fisher Scoring iterations: 5

I will then look at our selection criterion, the Akaike Information Criterion (AIC) and Bayesian Information Criterion (BIC). For all of the analysis in the report, I will choose to use forward stepwise regression to minimize the AIC. It is also important to note that while both selection criterion was calculated, only the AIC was used to decide model selection due to the fact the it does not penalize complexity as much as BIC. With the context of this data, a false negative would be more harmful, in that if I conclude that something like the length of employment does not predict the odds of contracting byssinosis when in reality it does would be more harmful than concluding the opposite. Beginning with forward stepwise regression the model that minimizes this criterion we are suggested to be left with a model that includes workspace, employment, and smoking as predictors and excludes sex and race.

# AIC - additive model
bestforwardAIC=step(nullModel,scope = list(lower = nullModel, upper = fullModel),direction = "forward")
## Start:  AIC=431.2
## cbind(Byssinosis, Non.Byssinosis) ~ 1
## 
##              Df Deviance    AIC
## + Workspace   2    70.42 183.09
## + Sex         1   281.18 391.86
## + Smoking     1   301.11 411.78
## + Employment  2   312.29 424.97
## + Race        1   316.50 427.18
## <none>            322.53 431.20
## 
## Step:  AIC=183.09
## cbind(Byssinosis, Non.Byssinosis) ~ Workspace
## 
##              Df Deviance    AIC
## + Employment  2   55.315 171.99
## + Smoking     1   58.414 173.09
## + Race        1   67.965 182.64
## <none>            70.419 183.09
## + Sex         1   69.761 184.44
## 
## Step:  AIC=171.99
## cbind(Byssinosis, Non.Byssinosis) ~ Workspace + Employment
## 
##           Df Deviance    AIC
## + Smoking  1   43.882 162.56
## <none>         55.315 171.99
## + Race     1   55.005 173.68
## + Sex      1   55.293 173.97
## 
## Step:  AIC=162.56
## cbind(Byssinosis, Non.Byssinosis) ~ Workspace + Employment + 
##     Smoking
## 
##        Df Deviance    AIC
## <none>      43.882 162.56
## + Race  1   43.563 164.24
## + Sex   1   43.586 164.26

Next, we’ll continue the analysis by again using forward stepwise regression in order to determine if I should include any interactions in our final model. We’ll set the scope of this stepwise regression be from an empty model to a model that includes all of our predictors and all of combinations of single term interactions between them. When looking at minimizing the AIC when I include interaction terms, when looking at the output below, I are left with a model that includes workplace, length of employment, smoking status, as well as an interaction between smoking status and workspace. The reason this does not include the interaction between sex and workspace that I discovered using the Wald test is most likely due to the fact that in order to include this interaction in our model, I would also have to include the predictor sex in the model. As I can recall, sex was not included when I minimized AIC when using only an additive model, so it is likely that including this interaction would decrease our AIC overall in order to include the interaction.

all.int.model = glm(cbind(Byssinosis,Non.Byssinosis) ~.^2, data = b.data,family = binomial())
## AIC - interactive model
bestforwardAICint=step(nullModel,scope = list(lower = nullModel, upper = all.int.model),direction = "forward")
## Start:  AIC=431.2
## cbind(Byssinosis, Non.Byssinosis) ~ 1
## 
##              Df Deviance    AIC
## + Workspace   2    70.42 183.09
## + Sex         1   281.18 391.86
## + Smoking     1   301.11 411.78
## + Employment  2   312.29 424.97
## + Race        1   316.50 427.18
## <none>            322.53 431.20
## 
## Step:  AIC=183.09
## cbind(Byssinosis, Non.Byssinosis) ~ Workspace
## 
##              Df Deviance    AIC
## + Employment  2   55.315 171.99
## + Smoking     1   58.414 173.09
## + Race        1   67.965 182.64
## <none>            70.419 183.09
## + Sex         1   69.761 184.44
## 
## Step:  AIC=171.99
## cbind(Byssinosis, Non.Byssinosis) ~ Workspace + Employment
## 
##                        Df Deviance    AIC
## + Smoking               1   43.882 162.56
## <none>                      55.315 171.99
## + Race                  1   55.005 173.68
## + Sex                   1   55.293 173.97
## + Employment:Workspace  4   50.504 175.18
## 
## Step:  AIC=162.56
## cbind(Byssinosis, Non.Byssinosis) ~ Workspace + Employment + 
##     Smoking
## 
##                        Df Deviance    AIC
## + Smoking:Workspace     2   39.031 161.71
## <none>                      43.882 162.56
## + Race                  1   43.563 164.24
## + Sex                   1   43.586 164.26
## + Employment:Smoking    2   42.077 164.75
## + Employment:Workspace  4   39.282 165.96
## 
## Step:  AIC=161.71
## cbind(Byssinosis, Non.Byssinosis) ~ Workspace + Employment + 
##     Smoking + Workspace:Smoking
## 
##                        Df Deviance    AIC
## <none>                      39.031 161.71
## + Race                  1   38.755 163.43
## + Employment:Smoking    2   36.772 163.45
## + Sex                   1   38.953 163.63
## + Employment:Workspace  4   34.291 164.97

After using these techniques in model selection, I will decide on a final model that was suggested by the AIC when including interactive terms. This was a model that included the dustiness of workspace, length of employment, smoking status, and an interaction between dustiness of workspace and smoking status. Table 1 displays the coefficients for our final model chosen by forward stepwise regression based on the Akaike Information Criterion.

final.model = glm(cbind(Byssinosis,Non.Byssinosis) ~Workspace + Employment + Smoking + Workspace*Smoking, data = b.data,family = binomial())
summary(final.model)$coefficients
##                         Estimate Std. Error    z value     Pr(>|z|)
## (Intercept)           -2.7146022  0.2645170 -10.262485 1.039955e-24
## Workspace2            -1.7769484  0.4176649  -4.254483 2.095324e-05
## Workspace3            -2.3461198  0.3727790  -6.293594 3.101979e-10
## Employment>=20         0.6638259  0.1819389   3.648619 2.636534e-04
## Employment10-19        0.4989688  0.2499100   1.996594 4.586933e-02
## SmokingYes             0.9572850  0.2750856   3.479953 5.015019e-04
## Workspace2:SmokingYes -1.1806748  0.5489627  -2.150738 3.149691e-02
## Workspace3:SmokingYes -0.4864177  0.4338355  -1.121203 2.622014e-01

The using the above coefficients, the formula for the final model that given by:

\(\log(\frac{\pi}{1-\pi}) = -2.7146 + (-1.7769)X_{Workspace, less dusty}\)

$+ (-2.3461)X_{Workspace, least dusty} + 0.6638X_{Employment, 20} + 0.4990X_{Employment, 10-19} $

$+ 0.9573X_{Smoking, yes} + (-1.1807)X_{Workspace, less dusty:Smoking, yes} $

\(+ (-0.4864)X_{Workspace, least dusty:Smoking, yes}\)

Furthermore, I can interpret the coefficients of the model in terms of their effect on the odds on the status of byssinosis using the values above. I can see that the indicator for employment greater than or equal to 10 and smoking status is no are the only three predictors that result in a positive effect on having byssinosis. Concurrently, the other variables result in the decrease of having byssinosis when all others are zero.

Summary

By making use of categorical data analysis, I can conclude that the dustiness of workspace, length of employment, and smoking status are all significant factors to consider when trying to predict if a worker in these conditions would contract byssinosis. Through the analysis of this data I have determined that there is also a significant interaction between dustiness of workspace and smoking status that would be important to take into account in this model. By taking into account both the AIC and BIC I was able to get a full picture on how to best to fit our model without over or under simplifying our model with the hope of making use of further predictions of incidence of this lung disease.